Orice porţiune a unui circuit electric comunică cu restul circuitului printr-un număr oarecare de borne. Cea mai simplă situaţie este cazul în care porţiunea de circuit este un dipol. Dacă dipolul este pasiv (nu conţine generatoare), fiind format numai din rezistoare, atunci el poate fi înlocuit cu un singur rezistor, numit rezistor echivalent, astfel încât restul circuitului să nu "simtă" înlocuirea.
Un rezistor este echivalent unei grupări de rezistoare dacă, la aplicarea aceleiaşi tensiuni la bornele rezistorului echivalent ca şi la bornele grupării, circulă un curent electric cu aceeaşi intensitate.
Două sau mai multe rezistoare sunt conectate în serie dacă aparţin aceleiaşi ramuri dintr-o reţea electrică. Rezistoarele grupate în serie sunt parcurse de acelaşi curent electric.
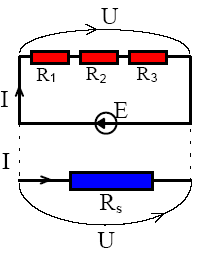
Considerând un grup de trei rezistori conectaţi în seie, la bornele fiecărui rezistur se va regăsi câte o tensiune U1;U2 si U3 incat se poate scrie:
U=U1+U2+U3
Pe baza legii lui Ohm pe fiecare rezistor rezulta:
U=IR1+IR2+IR3
sau
U=I(R1+R2+R3)
Aplicăm aceeaşi lege la circuitul echivalent:
U=IRs
Rezulta urmatoarea relatie: Rs=R1+R2+R3
În cazul general, când sunt conectate n rezistoare în serie
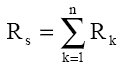
Rezistenţa echivalentă Rs este întotdeauna mai mare decât oricare dintre rezistenţele Rk.
Două sau mai multe rezistoare sunt grupate în paralel dacă sunt conectate între aceleaşi două noduri.
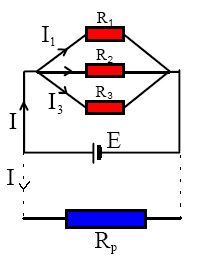
Rezistoarele grupate în paralel au aceeaşi tensiune la borne. Conform legii I a lui Kirchhoff I=I1+I2+I3
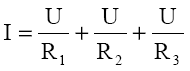
Pentru circuitul echivalent:
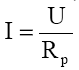
De unde rezulta:
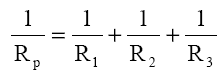
Sau în cazul în care sunt conectaţi în paralel n rezistori
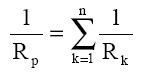
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
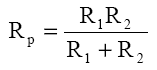
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.
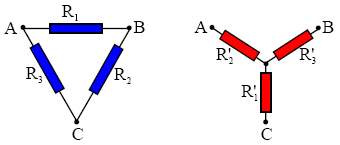
Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
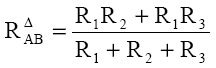
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
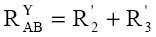
Impunând condiţia de echivalenţă a celor două circuite:
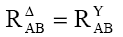
rezulta:
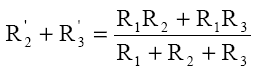
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
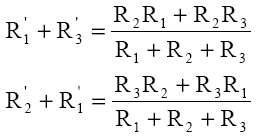
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
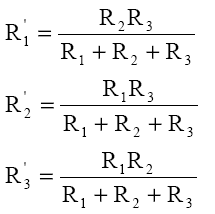
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.
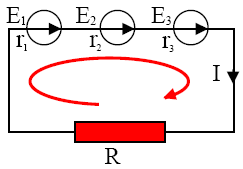
Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
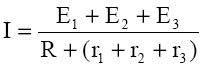
Prin comparaţie cu legea lui Ohm pe un circuit închis:
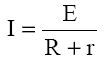
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.
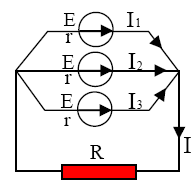
Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
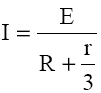
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
Două sau mai multe rezistoare sunt conectate în serie dacă aparţin aceleiaşi ramuri dintr-o reţea electrică. Rezistoarele grupate în serie sunt parcurse de acelaşi curent electric.

Considerând un grup de trei rezistori conectaţi în seie, la bornele fiecărui rezistur se va regăsi câte o tensiune U1;U2 si U3 incat se poate scrie:
U=U1+U2+U3
Pe baza legii lui Ohm pe fiecare rezistor rezulta:
U=IR1+IR2+IR3
sau
U=I(R1+R2+R3)
Aplicăm aceeaşi lege la circuitul echivalent:
U=IRs
Rezulta urmatoarea relatie: Rs=R1+R2+R3
În cazul general, când sunt conectate n rezistoare în serie
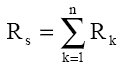
Rezistenţa echivalentă Rs este întotdeauna mai mare decât oricare dintre rezistenţele Rk.
Două sau mai multe rezistoare sunt grupate în paralel dacă sunt conectate între aceleaşi două noduri.

Rezistoarele grupate în paralel au aceeaşi tensiune la borne. Conform legii I a lui Kirchhoff I=I1+I2+I3
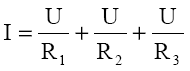
Pentru circuitul echivalent:
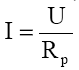
De unde rezulta:
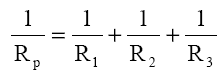
Sau în cazul în care sunt conectaţi în paralel n rezistori
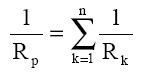
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
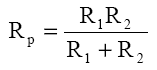
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
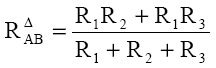
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
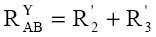
Impunând condiţia de echivalenţă a celor două circuite:
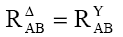
rezulta:
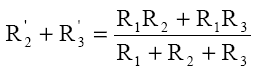
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
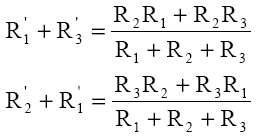
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
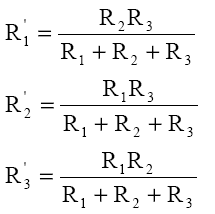
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
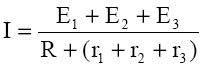
Prin comparaţie cu legea lui Ohm pe un circuit închis:
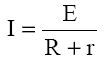
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
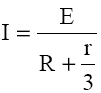
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.

Pe baza legii lui Ohm pe fiecare rezistor rezulta:
U=IR1+IR2+IR3
sau
U=I(R1+R2+R3)
Aplicăm aceeaşi lege la circuitul echivalent:
U=IRs
Rezulta urmatoarea relatie: Rs=R1+R2+R3
În cazul general, când sunt conectate n rezistoare în serie
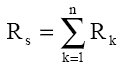
Rezistenţa echivalentă Rs este întotdeauna mai mare decât oricare dintre rezistenţele Rk.
Două sau mai multe rezistoare sunt grupate în paralel dacă sunt conectate între aceleaşi două noduri.

Rezistoarele grupate în paralel au aceeaşi tensiune la borne. Conform legii I a lui Kirchhoff I=I1+I2+I3
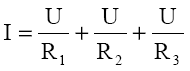
Pentru circuitul echivalent:
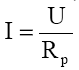
De unde rezulta:
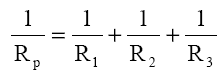
Sau în cazul în care sunt conectaţi în paralel n rezistori
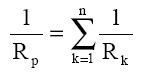
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
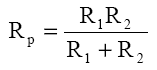
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
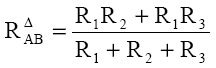
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
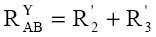
Impunând condiţia de echivalenţă a celor două circuite:
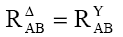
rezulta:
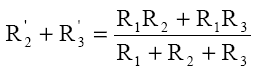
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
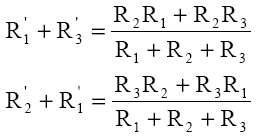
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
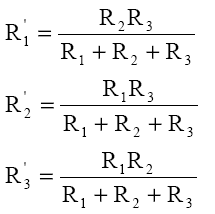
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
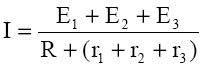
Prin comparaţie cu legea lui Ohm pe un circuit închis:
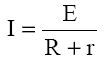
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
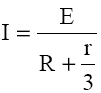
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
În cazul general, când sunt conectate n rezistoare în serie
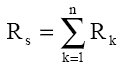
Rezistenţa echivalentă Rs este întotdeauna mai mare decât oricare dintre rezistenţele Rk.
Două sau mai multe rezistoare sunt grupate în paralel dacă sunt conectate între aceleaşi două noduri.

Rezistoarele grupate în paralel au aceeaşi tensiune la borne. Conform legii I a lui Kirchhoff I=I1+I2+I3
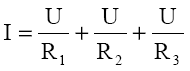
Pentru circuitul echivalent:
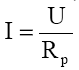
De unde rezulta:
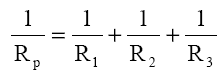
Sau în cazul în care sunt conectaţi în paralel n rezistori
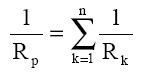
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
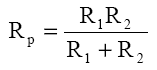
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
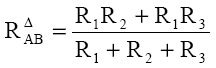
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
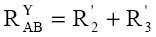
Impunând condiţia de echivalenţă a celor două circuite:
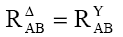
rezulta:
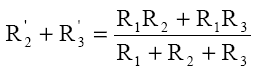
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
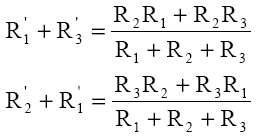
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
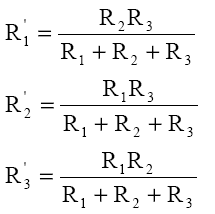
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
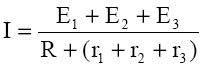
Prin comparaţie cu legea lui Ohm pe un circuit închis:
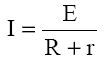
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
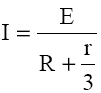
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
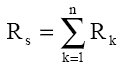
Două sau mai multe rezistoare sunt grupate în paralel dacă sunt conectate între aceleaşi două noduri.

Rezistoarele grupate în paralel au aceeaşi tensiune la borne. Conform legii I a lui Kirchhoff I=I1+I2+I3
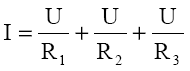
Pentru circuitul echivalent:
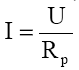
De unde rezulta:
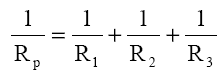
Sau în cazul în care sunt conectaţi în paralel n rezistori
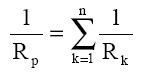
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
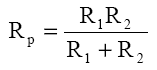
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
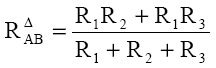
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
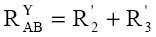
Impunând condiţia de echivalenţă a celor două circuite:
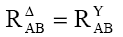
rezulta:
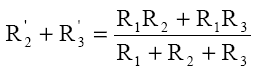
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
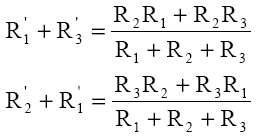
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
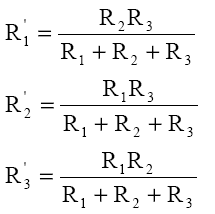
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
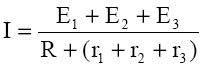
Prin comparaţie cu legea lui Ohm pe un circuit închis:
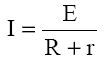
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
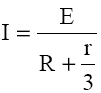
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.

Pentru circuitul echivalent:
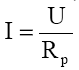
De unde rezulta:
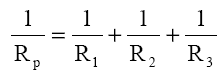
Sau în cazul în care sunt conectaţi în paralel n rezistori
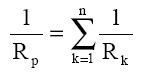
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
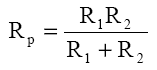
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
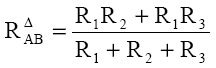
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
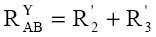
Impunând condiţia de echivalenţă a celor două circuite:
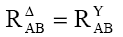
rezulta:
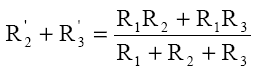
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
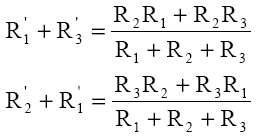
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
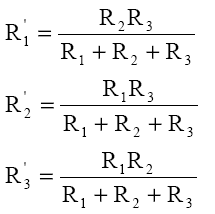
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
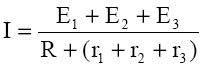
Prin comparaţie cu legea lui Ohm pe un circuit închis:
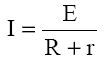
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
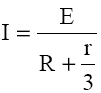
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
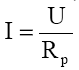
Sau în cazul în care sunt conectaţi în paralel n rezistori
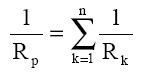
Rezistenţa echivalentă Rp este întotdeauna mai mică decât oricare din rezistanţele Rk. Pentru cazul în care sunt conectate doar două rezistoare în paralel este comod de calculat rezistenţa echivalentă folosind relaţia
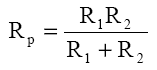
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
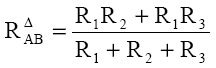
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
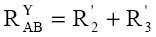
Impunând condiţia de echivalenţă a celor două circuite:
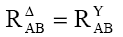
rezulta:
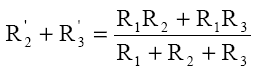
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
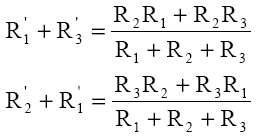
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
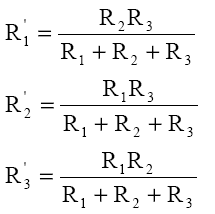
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
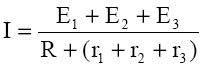
Prin comparaţie cu legea lui Ohm pe un circuit închis:
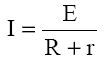
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
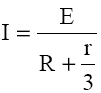
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
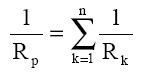
Dacă o porţiune de circuit comunică cu restul circuitului prin trei borne, structurile cele mai simple sunt: gruparea în triunghi şi gruparea stea.

Se poate demonstra că cele două grupări sunt echivalente dacă şi numai dacă ele sunt echivalente în raport cu oricare două dintre borne, a treia fiind neconectată ("în aer"). Pentru gruparea triunghi, în raport cu bornele A şi B, rezistanţa echivalentă este:
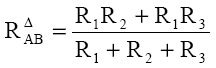
La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
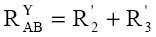
Impunând condiţia de echivalenţă a celor două circuite:
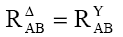
rezulta:
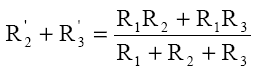
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
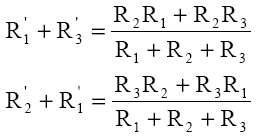
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
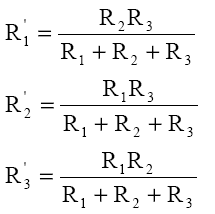
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
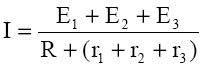
Prin comparaţie cu legea lui Ohm pe un circuit închis:
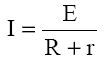
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
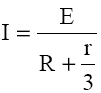
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.

La gruparea stea, în raport cu bornele A şi B (cu borna C neconectată) rezistenţa echivalentă este:
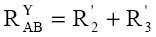
Impunând condiţia de echivalenţă a celor două circuite:
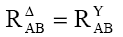
rezulta:
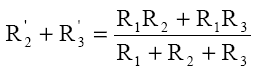
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
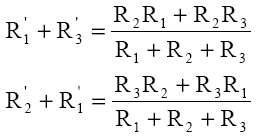
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
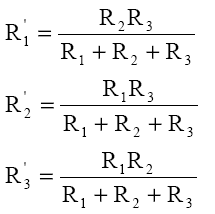
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
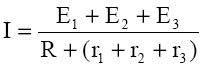
Prin comparaţie cu legea lui Ohm pe un circuit închis:
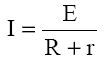
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
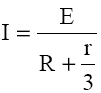
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
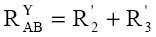
rezulta:
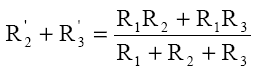
Relaţiile corespunzătoare celorlalte perechi de puncte: B şi C apoi C şi A.
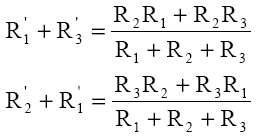
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
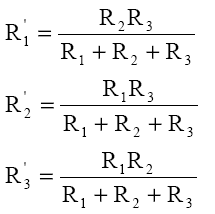
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
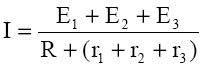
Prin comparaţie cu legea lui Ohm pe un circuit închis:
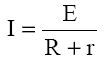
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
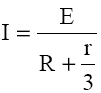
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
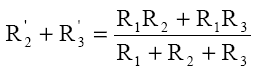
Rezolvăm sistemul de ecuaţii în raport cu rezistenţele R1', R2' şi R3'. Obtinem:
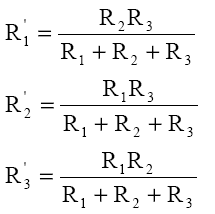
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
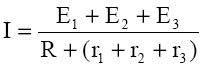
Prin comparaţie cu legea lui Ohm pe un circuit închis:
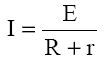
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
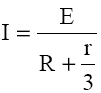
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
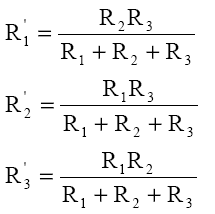
Pentru agrupa în serie mai multe generatoare se leagă borna negativă a unui generator cu borna pozitivă a următorului generator ş.a.m.d.

Sa consideram trei generatoare cu t.e.m. E1; E2 si E3 si cu rezistentele interne r1, E1 si E1, conectate in serie si care alimenteaza un consumator rezist R. Prin aplicarea legii a II-a a lui Kirchhoff pe circuitul dat, se obtine: E1+E2+E3=IR+Ir1+Ir2+Ir3. De unde:
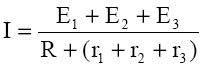
Prin comparaţie cu legea lui Ohm pe un circuit închis:
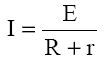
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
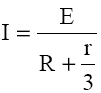
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.

Prin comparaţie cu legea lui Ohm pe un circuit închis:
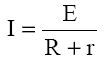
se constată că prin legarea în serie a generatoarelor:
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
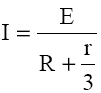
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
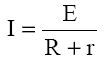
- tensiunea electromotoare este egală cu suma t.e.m. a generatoarelor: E=E1+E2+E3
- rezistenţa internă este egală cu suma rezistenţelor generatoarelor: r=r1+r2+r3
Pentru gruparea paralel ageneratoarelor, se leagă la un loc bornele pozitive şi de asemenea se leagă împreună bornele negative.

Considerăm trei generatoare identice cu t.e.m. E şi rezistenţa interioară r, grupate în paralel şi care alimentează un consumator cu rezistenţa R. Aplicând legile lui Kirchhoff pe circuit se obţin:
I=I1+I2+I3
E=I1r+IR
Dar: I1=I2=I3 deci I=3I1
Rezulta:
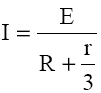
Se constată că t.e.m. este E dar rezistenţa internă devine r/3.
